吃什么药可以延长时间

百度 总之，书法的热闹，虽然会出现一些偏差，但现代社会需要它。

無差別曲線（むさべつきょくせん、英: indifference curve）は、消費者の選好関係の幾何学的表現で、同等に好ましい、または、同じ効用が得られる消費計画を結んだ曲線。等効用線ともいう。消費者行動の分析に用いられる。

無差別曲線の例
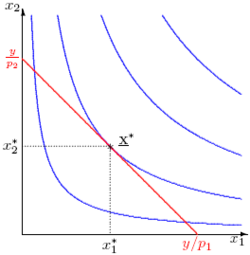
青が無差別曲線、赤で示すものが予算線であり、ここでは$x^{*}$において効用が最大化している。

選好関係が標準的な公理を満たすとき、無差別曲線は、右下がりで、原点に向かって凸の曲線となる。

一般的に消費者は、無差別曲線と予算線と無差別曲線が接するところ（最適消費計画と呼ぶ）で効用を最大化する。無差別曲線と予算線が接するということは、限界代替率が相対価格と等しくなることを意味する。

所得が変動したときの最適消費計画の軌跡を所得消費曲線と呼ぶ。 財の価格が変動したときの最適消費計画の軌跡を価格消費曲線と呼ぶ。

価格変動時における最適消費計画の移動は代替効果と所得効果に分解できる。代替効果とは、財の相対価格の変化による消費量の変化を示し、所得効果とは、価格変化がもたらす実質所得の変化による消費量の変化を示す。この分解はスルツキー分解と呼ばれ、スルツキー方程式で表される。

歴史

無差別曲線の理論は、フランシス?イシドロ?エッジワースによって発展され、彼は1881年の著書でその作図に必要な数学を説明した。その後、ヴィルフレード?パレートが1906年の著書でこれらの曲線を実際に描いた最初の人物であった。この理論は、個人が常に消費バンドルを選好の順序で順位付けできるとするウィリアム?スタンレー?ジェヴォンズの順序効用理論から導かれることができる。

地図と性質

効用関数の等高線として得られる無差別曲線の例

複数の効用水準に対する無差別曲線のグラフは無差別地図と呼ばれる。異なる効用水準をもたらす点はそれぞれ異なる無差別曲線に対応し、これらの無差別曲線は地形図上の等高線に似ている。曲線上の各点は同じ「高さ」を表す。北東方向に移動すると（財の限界効用が正であると仮定）、効用の高い地点へ移動することになる。より高い位置ほど効用水準が高い。非飽和性の要件により、全てのバンドルよりも好まれる消費バンドル、すなわち至福点には到達しない。

無差別曲線は典型的に以下の性質を持つとされる:

1. 負のスロープを持つ（片方の財の消費を増やすと、効用を一定に保つために他方の財の消費を減らす必要がある）。
2. 全順序性：同一の無差別曲線上の全ての点は等しく選好され、それ以外の点と比較してより好まれるか、好まれないかのいずれかに分類される。
3. 推移律：高い無差別曲線上の全ての点は低い無差別曲線上の全ての点より好まれる。
4. 凸性：無差別曲線は原点に対して凸である。これは限界代替率逓減の法則と一致する。

消費者選好理論の仮定

• 選好は完全性を持つ。消費者は利用可能な全ての財の組み合わせを順位付けできる。
• 選好は反射性を持つ。同一のバンドルは等しく選好される。
• 選好は推移的である。
• 選好は連続性を持つ。効用関数は連続であり、無差別曲線も連続である。
• 強単調性：2つの財が共に多いバンドルはより好まれる。
• 限界代替率逓減：1財を追加的に得るために他財を犠牲にする意欲は、徐々に減少する。

応用

予算制約線と無差別曲線の接点で効用は最大化される

消費者理論では、無差別曲線と予算制約を用いて需要曲線を導出する。予算制約線と無差別曲線の接点が効用最大化点である。価格の変化は予算制約線の傾きを変化させ、新しい接点を生じさせ、需要量を変化させる。

無差別曲線の例

• 
  図1: 3つの無差別曲線の例
• 
  図2: 完全代替財の場合の無差別曲線
• 
  図3: 完全補完財の場合の無差別曲線

選好関係と効用

消費者は選好関係で形式的に表現され、無差別曲線は等しい選好の組み合わせを示す。

効用理論との関連

効用関数 $U(x,y)$ はバンドル $(x,y)$ を順位付けする関数であり、その等高線が無差別曲線となる。限界効用の比は無差別曲線の絶対値の傾き、すなわち限界代替率を表す。

例

• 線形効用：$U(x,y)=\alpha x+\beta y$
• コブ＝ダグラス効用：$U(x,y)=x^{\alpha }y^{1-\alpha }$
• CES効用：$U(x,y)=\left(\alpha x^{\rho }+(1-\alpha )y^{\rho }\right)^{1/\rho }$

批判

無差別曲線は効用理論一般に向けられる批判を継承している。ハーバート?ホーブンカンプは保有効果の存在が厚生分析に重大な影響を与えると主張し、マレー?ロスバードは「無差別曲線は実際の交換で観察されないため、客観的意味を持たない」と批判した。

参考文献

• Bruce R. Beattie and Jeffrey T. LaFrance, "The Law of Demand versus Diminishing Marginal Utility" (2006). Review of Agricultural Economics. 28 (2), pp. 263–271.
• Volker B?hm and Hans Haller (1987). "demand theory," The New Palgrave: A Dictionary of Economics, v. 1, pp. 785–92.
• John Geanakoplos (1987). "Arrow-Debreu model of general equilibrium," The New Palgrave: A Dictionary of Economics, v. 1, pp. 116–24.
• Binger and Hoffman (1998), Microeconomics with Calculus, 2nd ed. Addison-Wesley.
• Perloff (2008). Microeconomics, theory & Applications with Calculus. Addison-Wesley.
• Silberberg and Suen (2000). The Structure of Economics A Mathematical Analysis, 3rd ed. McGraw-Hill.
• Lipsey, Richard G. (1975). An introduction to positive economics (fourth ed.). Weidenfeld & Nicolson. pp. 214–7. ISBN 0-297-76899-9 -->